CRC32

logicname sample

{ -------------------------------------- }
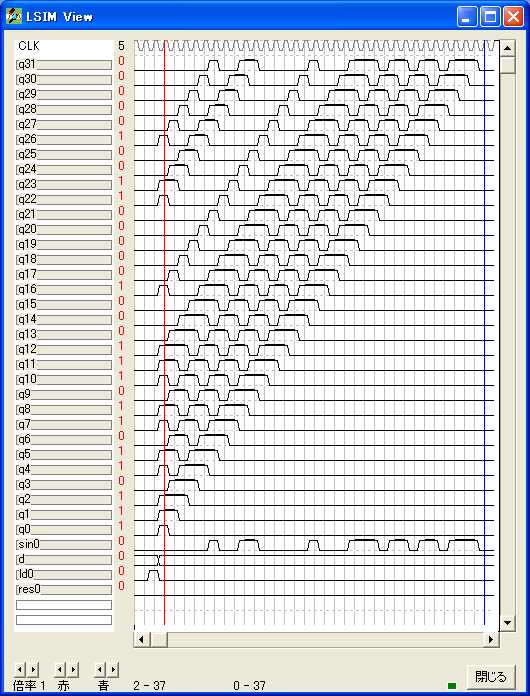
{    実効譜                              }
{ -------------------------------------- }
entity crc32
input  res,ld;
input  d[32];
input  sin;
output q[32];
bitr   rq[32];

   if (res)
      rq = 0;
   else
      if (ld)
         rq = d;
      else
         rq.0  = rq.31 ^ sin;
         rq.1  = rq.0  ^ (rq.31 ^ sin);
         rq.2  = rq.1  ^ (rq.31 ^ sin);
         rq.4  = rq.3  ^ (rq.31 ^ sin);
         rq.5  = rq.4  ^ (rq.31 ^ sin);
         rq.7  = rq.6  ^ (rq.31 ^ sin);
         rq.8  = rq.7  ^ (rq.31 ^ sin);
         rq.10 = rq.9  ^ (rq.31 ^ sin);
         rq.11 = rq.10 ^ (rq.31 ^ sin);
         rq.12 = rq.11 ^ (rq.31 ^ sin);
         rq.16 = rq.15 ^ (rq.31 ^ sin);
         rq.22 = rq.21 ^ (rq.31 ^ sin);
         rq.23 = rq.22 ^ (rq.31 ^ sin);
         rq.26 = rq.25 ^ (rq.31 ^ sin);

         rq.3 = rq.2;
         rq.6 = rq.5;
         rq.9 = rq.8;
         rq.13:15 = rq.12:14;
         rq.17:21 = rq.16:20;
         rq.24:25 = rq.23:24;
         rq.27:31 = rq.26:30;
      endif
   endif

   q = rq;
ende

{ -------------------------------------- }
{    機能実行譜                          }
{ -------------------------------------- }
entity sim
output res,ld;
output d[32];
output sin;
output q[32];
bitr   tc[8];
bitr   td[32];

   part crc32(res,ld,d,sin,q)

   tc=tc+1;

   if (tc<4)
      d.24:31=0b00000100;   {←初期値データ}
      d.16:23=0b11000001;
      d.8:15 =0b00011101;
      d.0:7  =0b10110111;
   endif

   if (tc<4)
      td.24:31=0b00000100;  {←テストデータ}
      td.16:23=0b11000001;
      td.8:15 =0b00011101;
      td.0:7  =0b10110111;
   else
      td.1:31=td.0:30;
   endif

   if (tc==3) ld=1; endif   {←初期値導入}

   sin=td.31;   {←テストデータ入力}
ende

endlogic