四桁の乗算器 その弐

ひとつの加算器を使う記憶型の乗算器です。

記憶型の論理なので初期化が必要です。 初期化で a を ra に b を rb に記憶します。 ra は上位に桁移動して b.0 の値によっては rq に加 算されます。 rb は下位に桁移動して rb.0 に加算を判定する b の 桁値を供給します。 

logicname sample

{ -------------------------------------- }
{    実効譜                              }
{ -------------------------------------- }
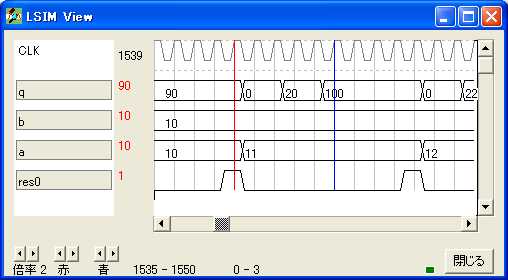
entity mul4
input  res;
input  a[4],b[4];
output q[8];
bitr   ra[8],rb[4];
bitr   rq[8];

   if (res)
      ra.0:3=a.0:3;
      rb=b;
      rq=0;
   else
      rb.0:2=rb.1:3;
      ra.1:7=ra.0:6;

      if (rb.0)
         rq=rq+ra;
      else
         rq=rq;
      endif
   endif

   q=rq;

ende

{ -------------------------------------- }
{    機能実行譜                          }
{ -------------------------------------- }
entity sim
output res;
output a[4],b[4];
output q[8];
bitr   tc[4];
bitr   ta[4],tb[4];

   part mul4(res,a,b,q)

   if (tc.3) tc=0; else tc=tc+1; endif

   if (tc.3) res=1; endif

   if (tc.3)
      ta=ta+1;
   else
      ta=ta;
   endif

   if ((tc.3)&(ta==15)) tb=tb+1; else tb=tb; endif

   a=ta;
   b=tb;
ende

endlogic

res が 1 のときに a の 10 と b の 10 を記憶して 10 × 10 = 100 を 初期化(赤線)から完了(青線)まで5クロックかかって 計算しています。


機能実行の全結果の PDF です。
四桁以上の乗算器では加算器がひとつで済む記憶型の 方が論理が小さくて済みます。
ただし桁数分のクロック数が必要になります。